不知道多久之前就说要写一些关于深度学习的笔记，结果被各种事情导致一拖再拖（当然也有自己懒的因素）。直到今天看完Andrej Karpathy的第三节课，我深知若再不记录，我只会学一点忘一点……

Pytorch Internals

Pytorch Internals
我这里主要记录关于pytorch中的核心数据结构——张量，其他内容大家感兴趣可以详细阅读上面讲解pytorch内部原理的博客。

张量是pytorch的核心数据结构，他由数据和元数据构成。元数据包括张量的大小，数据类型，张量所依赖的设备（CPU or CUDA?）和步幅。其中步幅（strides）是pytorch的特色之一。

每个张量都是线性存储的。我们以二维的tensor举例，实际上每个数据的内存位置都是连续的。那么pytorch引入步幅这一元数据的作用是什么？

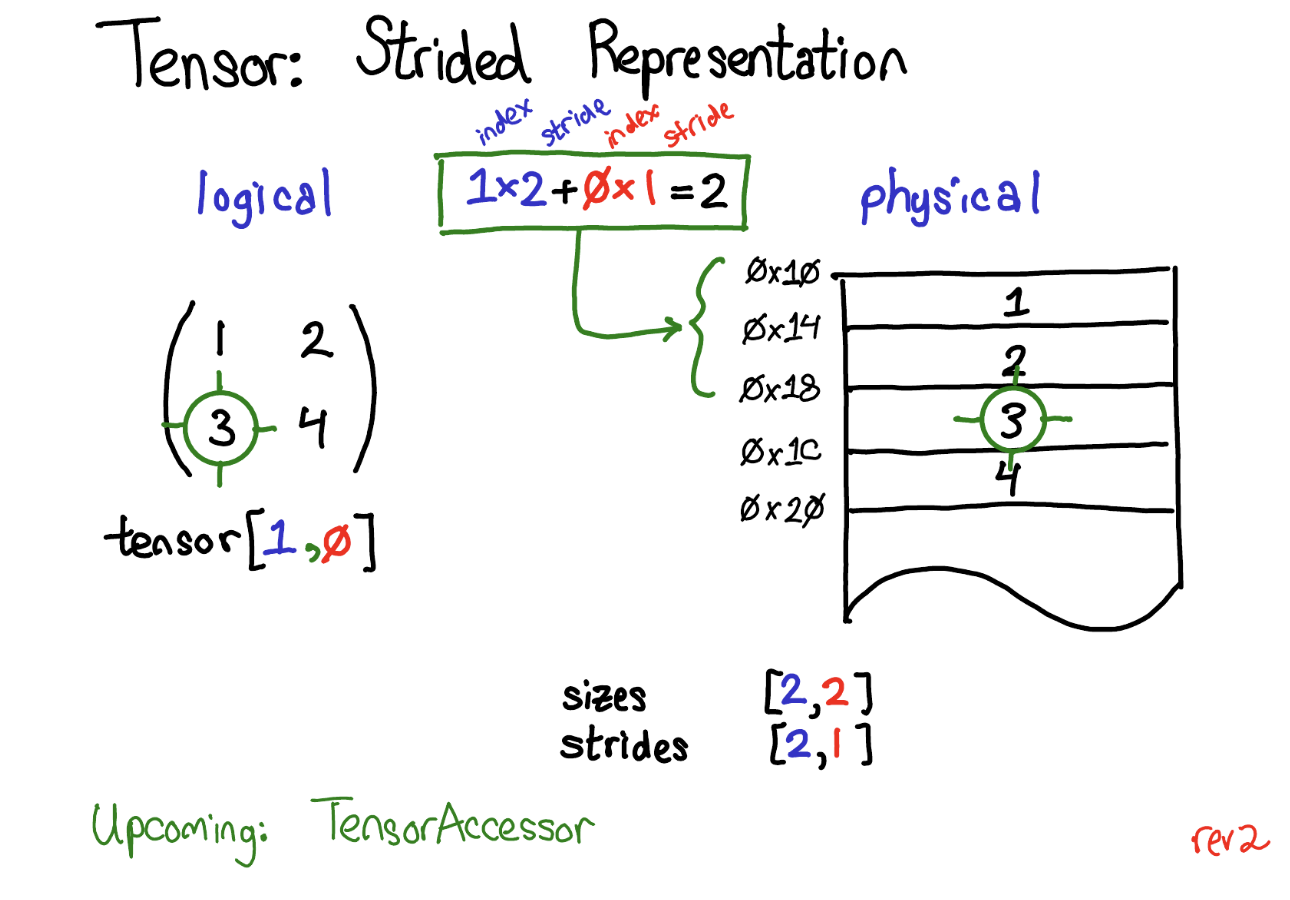
Strides
如上图，我们想要获取二维张量中(1，0)位置的数据，此时，每个维度x对应的步幅大小则为$2^x$，我们将索引和对应步幅大小乘积并求和，最后便能得到在我们想要的数据在线性内存中的位置。

步幅很有意思的应用在于，我们获取一列的数据不再需要利用循环。还是上图中的2维tensor，其中的第二列数据，通过tensor(:,1)便能很方便的获取。获取一行的数据也是类似，比如第一行，则为tensor(1,:)。

Broadcasting 广播机制

在pytorch以及numpy中，广播机制允许在进行逐元素操作时，使形状不同的张量兼容，而无需手动扩展张量的维度。广播的目的是避免显式地复制数据，节省计算资源。

广播的规则有以下四点：

  • 如果两个张量的形状不同，pytorch会从后往前（右对齐）匹配，如果无法匹配，说明两个张量形状不兼容，无法广播，pytorch则会报错。
  • 可以广播的条件：维度相等或其中一个张量的维度为1。
  • 如果一个维度为1，则会沿着该维度进行扩展（但不会复制数据）。
  • 如果某个张量缺少某个维度，pytorch会在该维度自动补充1。

下面给出一个多维度广播的示例：

1
2
3
4
5
6
7
A = torch.tensor([[[1, 2, 3]], [[4, 5, 6]]])  # 形状 (2, 1, 3)
B = torch.tensor([10, 20, 30])  # 形状 (3,)
C = A + B
print(C)

# 输出：tensor([[[11, 22, 33]],
        [[14, 25, 36]]])

One-Hot Encoding 独热编码

在机器学习中，我们通常会遇到分类问题。例如：[‘Blue’, ‘Green’, ‘Red’]，我们当然可以使用[0, 1, 2]的方式对这三个颜色特征进行编码，以区分它们。但这种方式会带来问题：三个颜色之间并非等距，存在偏序关系。这种编码会使得计算机学习到一些我们并不期望得到的特征，比如认为蓝色和绿色比起蓝色和红色相似度更高，因为它们之间距离更近。

独热编码就避免了这个问题的发生。它主要是采用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候只有一位有效。

仍然是上面的例子，[‘Blue’, ‘Green’, ‘Red’]一共三种颜色，所以采用三位状态寄存器进行编码，得到:

  • Blue $\rightarrow$ 001
  • Green $\rightarrow$ 010
  • Red $\rightarrow$ 100

我们可以看到，这三个编码互相是等距的，均为$\sqrt2$，说明它们之间具有相同的特性（均是颜色），不存在偏序关系，避免了第一种编码所出现的问题。

那么什么情况下不使用独热编码？

  • 当特征之间距离定义合适，存在偏序关系时，我们不适用独热编码。比如一个人的受教育程度，分为小学，初中，高中，大学，此时我们简单的使用[0, 1, 2, 3]进行编码即可。
  • 在决策树中，即使变量之间不存在任何偏序关系，我们通常也不使用独热编码。因为每个分叉仅决定“是否属于某个类别”，不关心数值的大小，所以简单的编码即可。

如何理解偏差，方差和噪声

参考博客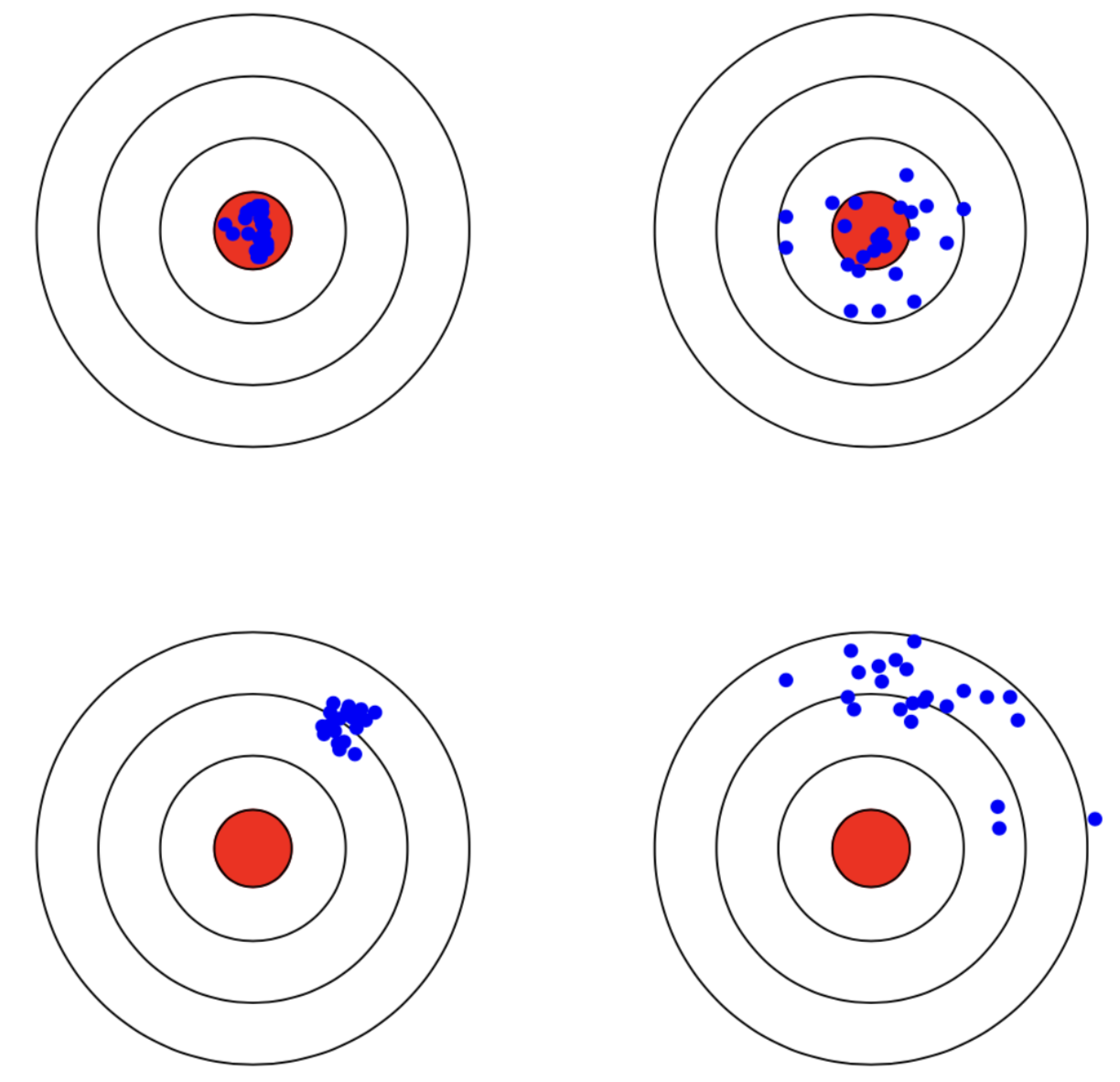
Bias
如上图，红色区域是学习算法完美的正确预测值，蓝色点为每个数据集所训练出的模型对样本的预测值。对于方差，蓝色点越集中，方差越小。对于偏差，蓝色点越偏离红色区域，偏差则越大，预测效果越差。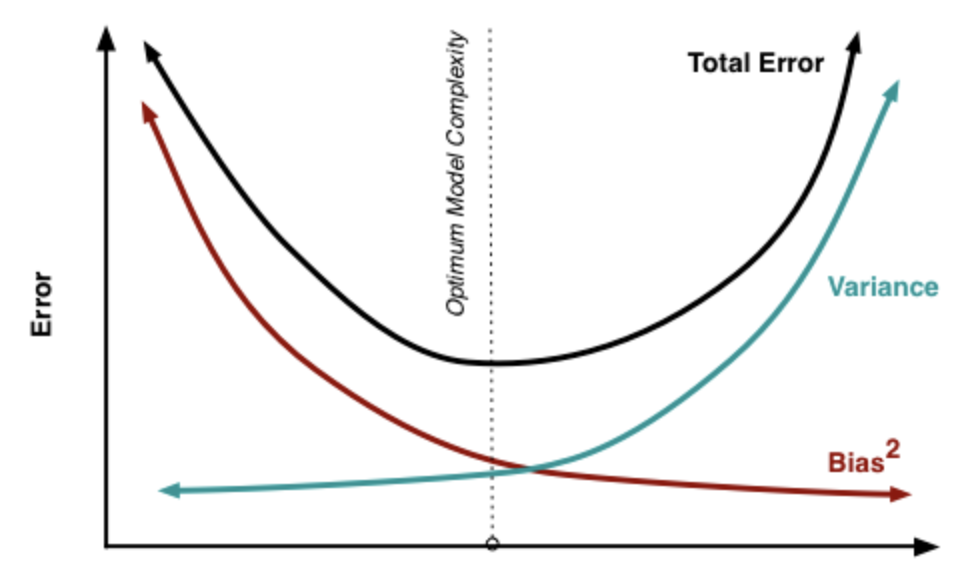
Performance
偏差和方差可以与欠拟合和过拟合进行比较：训练初期，欠拟合，学习器的拟合能力不够强，偏差比较大。在充分训练后，学习器的拟合能力非常强，训练数据的轻微扰动都会导致学习器发生显著变化，过拟合，方差大。

噪声是指数据中无法避免的随机误差，主要包括标签错误、特征测量误差、环境干扰等，反映了数据本身的可靠性问题。

总结：

  • 偏差： 度量学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
  • 方差： 度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所产生的影响。
  • 噪声： 表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。

残差连接 Residual Connection

在Transformer架构中，处处可以看到残差连接的身影，这是一种如今在深度学习模型中经常使用的技术，旨在解决梯度消失。残差连接首次由何恺明等人在2015年的论文《Deep Residual Learning for Image Recognition》中提出。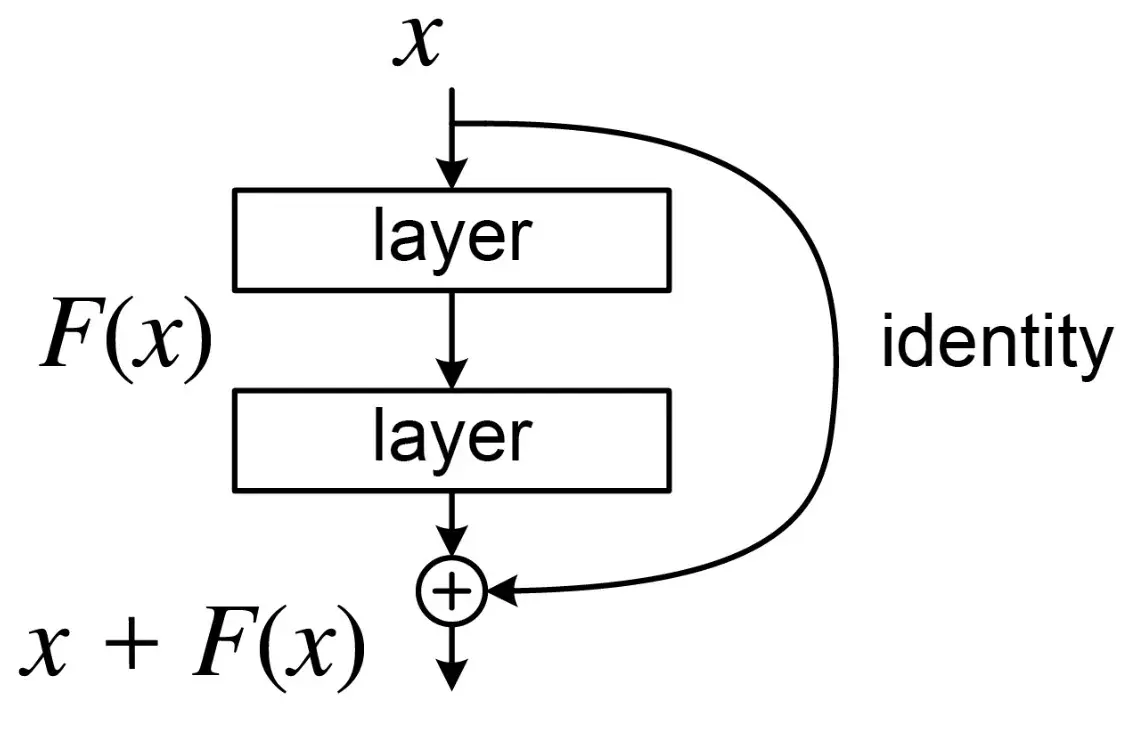
Residual
上图是残差连接的结构。我们可以看到残差连接实际上是建立了输入输出之间的一条捷径，一条“高速公路”。假设输入为x，经过非线性变换后输出为F(x)，引入残差连接后，输出就变为了F(x) + x，模型此时只需要学习残差映射，即为F(x) = H(x) - x。

这样做的好处是，首先可以避免梯度的消失和爆炸。对于梯度爆炸，因为残差连接的引入，网络可以在需要时倾向于学习更简单的函数，输入直接恒等连接至输出，这样在反向传播时就避免了一次梯度的相乘，防止梯度爆炸的情况产生。而对于梯度消失，即使学习的过程中，残差映射的梯度消失了，输入也能传输至输出，上一层的梯度可以完好无损的传递到下一层。

其次，残差连接加快模型的收敛。上面提到了网络在需要时倾向于学习更简单的函数，在一些恒等映射或者接近于恒等映射的情况，这条“高速公路”将输入直接连接至输出，加快网络收敛，毕竟让复杂的非线性函数去学习恒等映射是相当困难的。

最后，残差连接具有很强的扩展性。在很多架构中都能看到残差连接的身影，它可以很轻松的加入到这些架构中。同时在训练很深的网络时，残差连接的特性使得网络可以维持性能。

评估技术

BLEU

BLEU（Bilingual Evaluation Understudy）是一种用于评估机器翻译质量的算法，通过比较机器翻译的结果与人工参考译文的相似度进行评分。BLEU的计算公式如下：

其中：

$w_n$为权重，通常采用均匀分布，即为$1/N$

BP为长度惩罚因子，用于惩罚长度过短的翻译。定义中$c$表示候选译文的长度，$r$表示有效参考译文的长度。

$p_n$是$n-gram$精度，是BLEU算法的核心，它用于衡量连续的$n$个词汇（通常为$1-gram$至$4-gram$）在候选译文和有效参考译文中的重叠度。下图是$p_n$计算的例子。
BLEU
我们可以看到，为了避免过度生成高频词，每个$n-gram$的计数不回超过其在单个参考译文中所出现的最大次数。

BLEU中为什么要对$p_n$使用$log$求和？

我个人的理解是，首先，随着$n$的增大，$p_n$是呈现指数级别的下降的，为了避免因为某个$n-gram$匹配度极低对整体评分影响过大，因此采用$log$求和。其次，如果我们将$w_n = 1/N$代入公式，我们可以发现是对$p_n$求几何平均数，使用$log$也可以避免连乘可能带来的浮点数下溢。